Understanding Neural Networks and Deep Learning: A Simple Guide for Everyone

Neural networks, the backbone of deep learning, have been around since 1944. Recent advancements in research and computational power, particularly GPUs, along with the availability of large datasets, have significantly accelerated their development and application. They are now pivotal in various technologies, including language models like ChatGPT, image recognition and generation, autonomous vehicles, healthcare diagnostics, and more.

This article explores how neural networks work and why they are essential in solving complex problems.

What problems do neural networks and deep learning solve?

Many of today's questions can be answered with mathematical functions. For instance, if you want to estimate the value of your car in 5 years' time, a simple function to do so could look like this:

$$\begin{equation*} \text{Future value} = \text{Purchase price} - (\text{Yearly deprecation} \cdot \text{Years of ownership}) \end{equation*}​$$

This linear function can be plotted as follows:

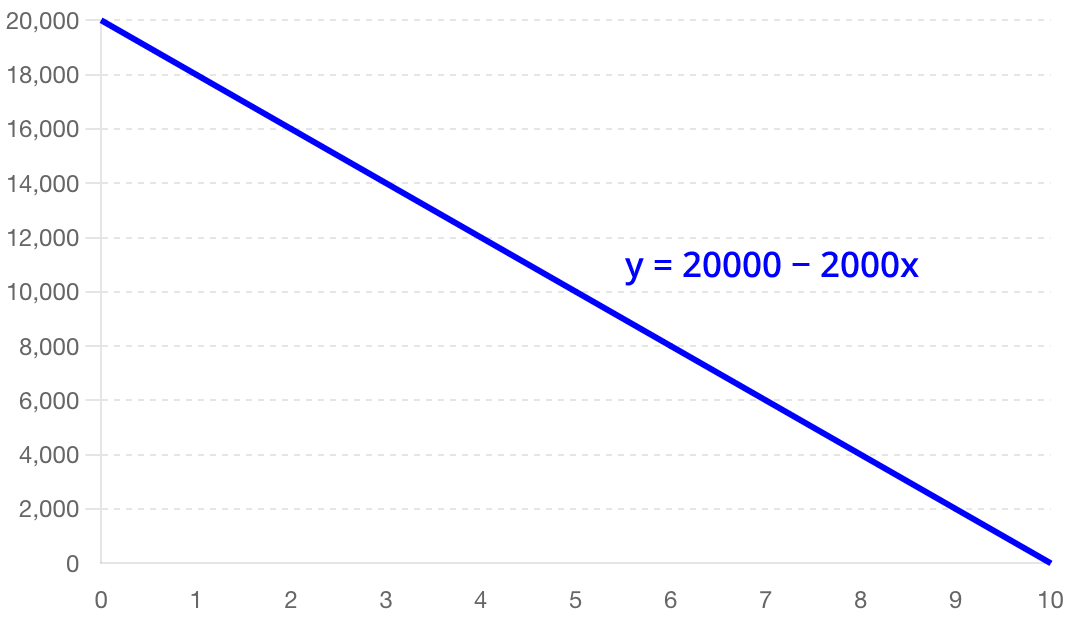
Our function takes an input (years of ownership) and gives an output (future value). For any given year, we can now calculate the future value.

This approach works well when all variables and their relationships are clearly defined. However, this is often not the case. Take rain forecasts, for example. Sophisticated weather models consider thousands of variables, from cloud cover to aerosol concentration. These variables influence each other, and the complexity of their interactions makes it difficult for humans to devise a function that effectively predicts rain.

This is where neural networks and deep learning come in. Using these tools and data, we can reverse engineer functions from the data.

In our car example, we had an input (years of ownership) and a function that produces an output (future value).

For rain prediction, we don't have a predefined function, but we have a lot of data. Over decades, we have collected thousands of input values (e.g., cloud cover or aerosol concentration) and corresponding outputs (e.g., rainfall).

By leveraging this historical data, we can instruct the computer to explore countless combinations and perform billions of calculations to derive a function that best correlates input variables with the output, in a process called "fitting."

Once we have a function, we can calculate the most likely output (e.g., rainfall) for any given values of input (e.g., weather conditions).

Here's a simplified illustration of this process for a dataset that only has one input and one output:

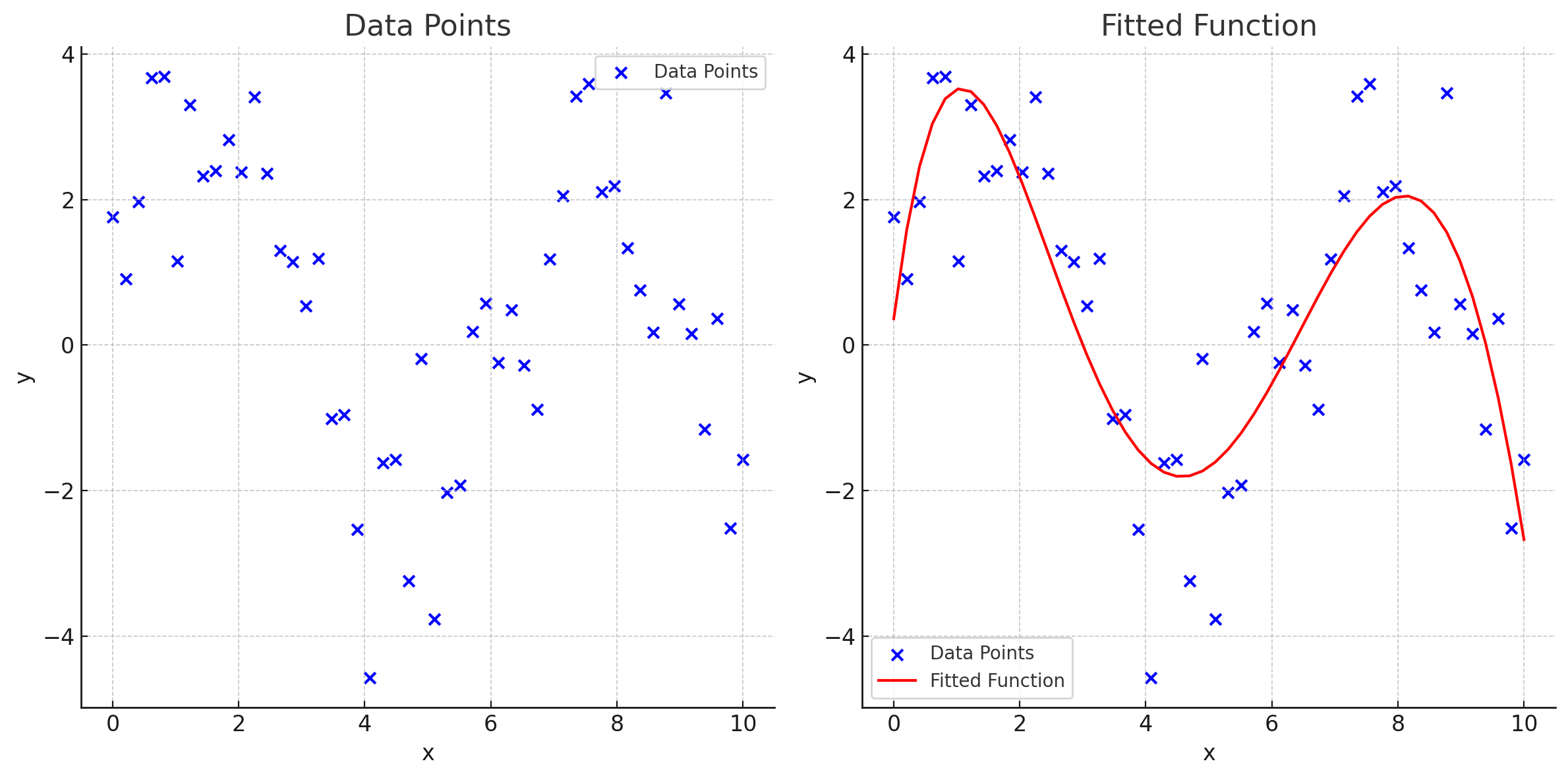
This fitted sample function above is a 5th-degree polynomial and can be expressed in mathematical terms as follows:

$$\begin{equation*} y = -0.0012x^5 + 0.0538x^4 - 0.7118x^3 + 4.1167x^2 - 6.1916x + 2.0334 \end{equation*}​$$

This function only takes one input, variable x. With our rain forecast, we have thousands of input variables, and they all influence each other.

To model this complexity, we can use neural networks.

What are neural networks?

Neural networks are structures used in machine learning to create complex functions from data for predictions and classifications. They do this by using linear algebra concepts, including matrices, to process and transform data through layers of interconnected neurons, which we will look at in more detail in sections below.

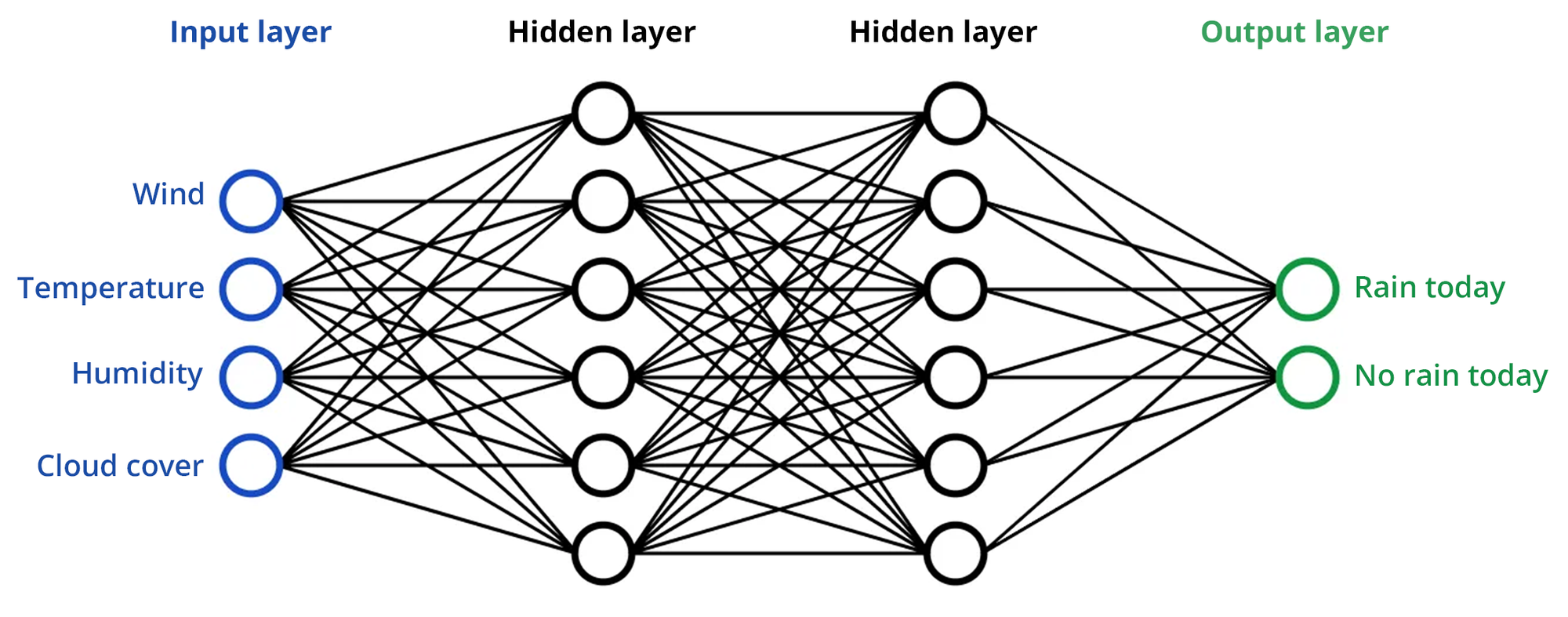
Neurons

Each circle in the illustration above represents a neuron. A neuron acts as a small computational unit and holds a number between 0 and 1. Neurons receive inputs, process them, and pass an output to the next layer.

• Input Neurons: Receive raw data from the external environment (e.g., wind, temperature, humidity, cloud cover in the weather prediction example).
• Hidden Neurons: Process inputs by applying a set of mathematical operations (like weighted sums and activation functions) to detect patterns and features in the data.
• Output Neurons: Produce the final output or prediction of the network (e.g., "Rain today" or "No rain today").
• Biases: Each neuron also has a bias term, which is an additional number added to the weighted sum of inputs. Biases help the model make better predictions by providing more flexibility in learning the data patterns.

Weights

Each line connecting neurons in different layers represents a weight. For instance, the connection between a wind input neuron and a hidden neuron has a specific weight in form of a number determining how much the wind input affects that hidden neuron.

Weights multiply the input values received by a neuron. If the weight is high, the input has a significant influence on the neuron's output; if it's low, the input has little influence.

Layers

Layers are collections of neurons grouped together within the network. A neural network typically consists of an input layer, one or more hidden layers, and an output layer. You can think of these like steps in a process.

• Input Layer: This is the first layer of the network, which directly receives the raw data (e.g. weather data). Each neuron in this layer represents an individual feature of the input data.
• Hidden Layers: These are the layers between the input and output layers. Each hidden layer neuron receives inputs from all neurons in the previous layer, processes these inputs, and passes the output to the next layer. The hidden layers are where most of the learning and pattern recognition occurs.
• Output Layer: The final layer produces the output of the network. For example, in a classification task, each neuron in the output layer might represent a different class, and the outputs can be interpreted as the probabilities of the input belonging to each class (e.g. whether it will rain today or not).

A neural network with more than one hidden layer is called a "deep neural network".

Deep learning: training the neural network with data

Deep learning is the process to train deep neural networks, those with more than one hidden layer, to make predictions and classifications from large amounts of data.

As the data moves through the layers, the connections between the nodes are strengthened or weakened, depending on the patterns in the data. This allows the network to learn from the data and make predictions or decisions based on what it has learned.

By adjusting the network's internal parameters — weights (which determine the strength of connections between neurons) and biases (which help adjust the output of the neuron along with the weighted sum) — we can reverse engineer a function that accurately maps input data to the desired output, enabling us to make predictions and classifications for new data of a similar kind.

Here’s how the process works:

1. Preparing the Data: We start with a dataset that includes input variables (features) like historical weather conditions and corresponding outputs (labels) such as whether it rained or not.
2. Initial Setup: The learning process begins by assigning random values to weights and biases.
3. Forward Propagation: The network processes the input data layer by layer. Each neuron calculates a value using the inputs, weights, and biases, eventually producing an output prediction in the output layer.
4. Evaluating Predictions: The accuracy of the prediction is measured using a loss function, which calculates the difference between the predicted and actual outputs.
5. Backpropagation: To minimise the error, the network undergoes backpropagation. This process calculates what is called a loss gradient and updates the weights and biases in the direction that reduces the error.
6. Iteration and Improvement: This cycle of forward propagation and backpropagation is repeated over many iterations, known as epochs, until the network’s performance improves sufficiently.

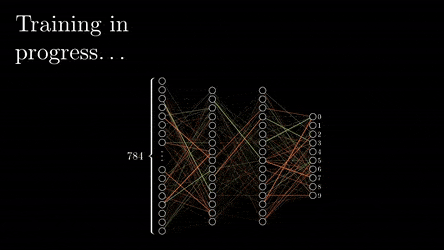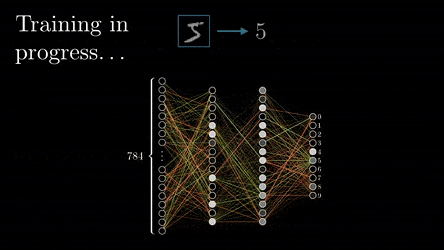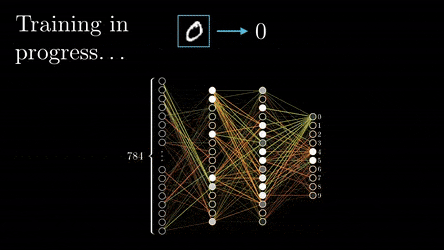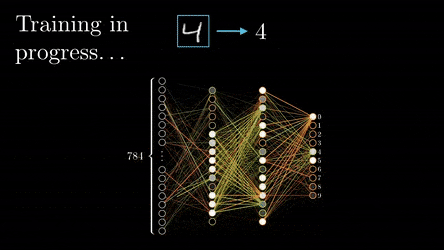
Once training is complete, the initially random weights and biases have been fine-tuned to accurately predict outcomes based on the input data. These optimised parameters can be saved, forming a pre-trained model. Some pre-trained models are available off the shelf and can be fine-tuned with additional training on specific data, making them quicker to adapt to new tasks because they already recognise general patterns after pre-training.

Deep learning models require substantial computational power and large datasets to train effectively. However, they excel at identifying complex patterns and making accurate predictions across various applications, from image recognition to natural language processing.

Check out this video for a more animated explanation of how neural networks and deep learning work: